450
Trùng trùng duyên khởi trong Toán học
Lê Hữu Dũng
Thật khó hiểu! Như vậy chúng là vô hình ư? Vô hình sao tạo nên vũ trụ hữu hình? Là hư vô? Hư vô sao lại tạo thành trùng trùng hiện hữu? Thế rồi bao nhiêu năm dài đằng đẵng trôi qua tôi mới dần ngộ ra.
Khi còn học phổ thông, tôi đọc trong một cuốn sách minh họa hình học: Điểm (như là) một “cái gì đó” không có “bề dày, bề rộng, bề ngang”, đường thẳng thì “dài” vô hạn, “mảnh” vô cùng, còn mặt phẳng thì “mỏng” vô cùng và “rộng” vô hạn. Thật khó hiểu! Như vậy chúng là vô hình ư? Vô hình sao tạo nên vũ trụ hữu hình? Là hư vô? Hư vô sao lại tạo thành trùng trùng hiện hữu? Thế rồi bao nhiêu năm dài đằng đẵng trôi qua tôi mới dần ngộ ra. Thì ra bài học vỡ lòng về hình học lại là một minh họa toán học cho tư tưởng Duyên khởi trong Phật pháp.
HỆ TIÊN ĐỀ HÌNH HỌC EUCLIDE
Thuật ngữ
Điểm: = A, B, C … Đường thẳng: = a, b, c, d… Mặt phẳng: = (P), (Q), (R)
Phần tử x thuộc tập A: =
Tập hợp A chứa trong tập hợp B: =
Tiên đề
1) Qua 2 điểm phân biệt tồn tại duy nhất 1 đường thẳng d.
2) Qua 3 điểm không cùng thuộc 1 đường thẳng, tồn tại duy nhất 1 mặt phẳng.
3) Nếu đường thẳng d có 2 điểm thuộc mặt phẳng (P) thì d chứa trong (P).
4) Nếu 2 mặt phẳng phân biệt có 1 điểm chung thì chúng có chung 1 đường thẳng gọi là giao tuyến của 2 mặt phẳng đó.
5) Trong mặt phẳng, qua 1 điểm không thuộc đường thẳng d, tồn tại duy nhất 1 đường thẳng không có điểm chung với d.
Như vậy, để “biết” điểm, đường thẳng, mặt phẳng, ngôn ngữ không thể bảo chúng là cái gì (what) mà phải mô tả thế nào (how) bằng một hệ tiên đề trong đó “điểm, đường thẳng, mặt phẳng” chỉ là các kí hiệu thuật ngữ, các quy ước đi kèm với các khái niệm “quan hệ” khác (tồn tại, thuộc, chứa trong) để nối kết chúng lại thông qua các tiên đề (công lý) mà ta công nhận không chứng minh. Cái này có bởi vì cái kia có. Không có cái nào có một hiện hữu tự thân. Điều này tương đồng kì lạ với tư tưởng “Duyên khởi” (Dependent origination) trong Đạo Phật: “Các hiện tượng tự thân chúng không là gì cả. Sở dĩ chúng có được bản chất của mình là nhờ vào sự phụ thuộc lẫn nhau. Tất cả đều duyên khởi từ Tánh không. Một trong tất cả, tất cả trong Một!” (trích dẫn Trịnh xuân Thuận – Vô hạn trong lòng bàn tay).
Với những “hạt” (điểm) và các “tương tác” (quan hệ) cơ bản, trong các tiên đề trên, thông qua thiết kế trùng trùng các khái niệm mới và định lý mới, các nhà toán học tạo nên một vũ trụ hình học Euclide sâu sắc, diệu kỳ. Xin hé mở một trong vô hạn những căn phòng ấn tượng của lâu đài kỳ vĩ đó:
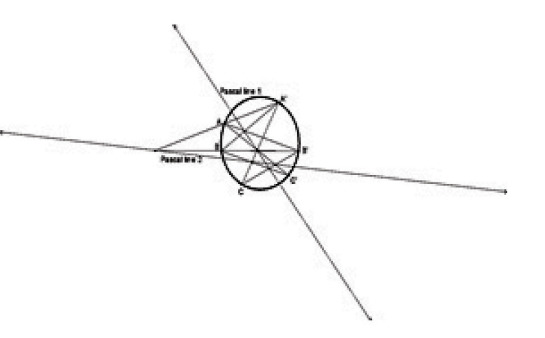
ĐỊNH LÝ PASCAL
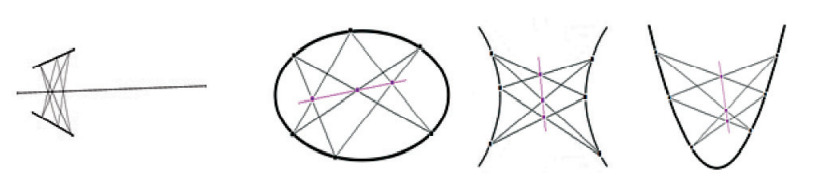
“Ba giao điểm của các cạnh đối diện của hình lục giác nội tiếp trong một conic nằm trên một đường thẳng (đường thẳng Pascal của lục giác)” (Blaise Pascal – nhà toán học Pháp)
Ứng với 6 điểm trên conic, ta có 60 lục giác khác nhau, phát sinh 60 đường thẳng Pascal khác nhau. Trong 60 đường đó, cứ 3 đường một đi qua 20 điểm gọi là điểm Steiner, các điểm này lại cứ 4 điểm một nằm trên 15 đường thẳng gọi là đường thẳng Plucker. Các đường Pascal cứ 3 đường một lại đồng quy trong một tập gồm 60 điểm khác gọi là các điểm Kirkman. Ứng với mỗi điểm Steiner có 3 điểm Kirkman sao cho cả 4 điểm đó đều nằm trên 1 đường thẳng gọi là đường thẳng Cayley. Có 20 đường thẳng Cayley như thế, trong đó cứ 4 đường một lại đi qua 15 điểm gọi là các điểm Salmon … Cứ thế, trùng trùng Duyên khởi, định lý Pascal mở ra những cảnh giới viên dung vô ngại. Tất cả đồng hiện trong một liên thông “Cục bộ – Toàn thể” hoàn hảo .
Tính khoa học của luật nhân quả
Điều này làm ta liên tưởng đến “Lưới trời Đế Thích” trong kinh Phật. Đó là một màn lưới làm bằng vô số viên ngọc trong suốt. Khi đứng trước vũ trụ làm bằng những vi trần ngọc sáng như gương ấy, hình ảnh của chúng ta hiện bóng khắp trong mỗi vi trần gương ngọc và mỗi vi trần gương ngọc lại phản chiếu lẫn nhau, thành ra một thế giới trùng trùng ảnh hiện. Tất cả là một, một là tất cả! Như diễn đạt của Thiền sư Khánh Hỷ đời Lý:
Càn khôn tận thị mao đầu thượng,
Nhật nguyệt bao hàm giới tử trung.
(Càn khôn ở trên đầu một sợi lông
Nhật nguyệt chứa trong lòng hạt cải).
Hoặc như thi sĩ người Anh William Blakes:
“To see a World in a Grain of Sand
And a Heaven in a Wild Flower,
Hold Infinity in the palm of your hand
And Eternity in an hour”.
(Để thấy vũ trụ trong một hạt cát
Và thiên đường trong một đóa hoa dại
Hãy nắm vô cùng trong lòng tay bạn
Và vĩnh cửu trong giây phút hiện tiền).
Tất cả là một, một là tất cả! Như diễn đạt của Thiền sư Khánh Hỷ đời Lý: “Càn khôn tận thị mao đầu thượng, Nhật nguyệt bao hàm giới tử trung”. (Càn khôn ở trên đầu một sợi lông Nhật nguyệt chứa trong lòng hạt cải).
CÙNG NHAU XIỂN DƯƠNG ĐẠO PHẬT
Tuân theo truyền thống Phật giáo, chúng tôi cung cấp tài liệu giáo dục Phật giáo phi lợi nhuận. Khả năng duy trì và mở rộng dự án của chúng tôi hoàn toàn phụ thuộc vào sự hỗ trợ của bạn. Nếu thấy tài liệu của chúng tôi hữu ích, hãy cân nhắc quyên góp một lần hoặc hàng tháng.
STK: 117 002 777 568
Ngân hàng Công thương Việt Nam
(Nội dung: Họ tên + tài thí Xiển dương Đạo Pháp)
TIN LIÊN QUAN
Dành cho bạn
Phật giáo Việt Nam và sự dung hợp tam giáo thời Trần
Nghiên cứu
14:00 30/11/2024
Có thể thấy, Phật giáo - Nho giáo và Đạo giáo đã có sự dung hòa, bổ sung cho nhau để cùng hướng đến xây dựng đời sống tinh thần và đời sống nhân văn cho xã hội.
Ứng dụng triết lý Phật giáo Trúc Lâm trong xây dựng, phát triển đất nước
Nghiên cứu
08:45 25/11/2024
Phật giáo là cuộc sống, không có sự phân biệt bất cứ thành phần nào trong xã hội, Phật giáo chính là quá trình đi tìm chân lý. Chân lý thì không nằm trong Phật giáo mà nằm trong cuộc sống.
Thiền phái Trúc Lâm Yên Tử: Dấu ấn của Phật giáo thời Trần
Nghiên cứu
09:40 15/11/2024
Thời đại nhà Trần, không những độc lập dân tộc, tự chủ về đời sống kinh tế, chính trị, xã hội…, mà còn độc lập, tự chủ về hệ tư tưởng làm chỗ dựa cho đời sống tinh thần của nhân dân Đại Việt thế kỷ XIII – XIV.
Tín ngưỡng thờ phụng đức Phật Dược Sư thời nhà Đường
Nghiên cứu
09:45 03/11/2024
Việc thiết lập đàn tràng và tu trì đức Phật Dược Sư trở nên quan trọng hơn dưới thời trị vì của vua Đường Túc Tông, thời kỳ triều đình nhà Đường phải vật lộn để vượt qua thách thức do những cuộc nổi dậy của quân đội trong nước gây nên...
Xem thêm
