Thứ năm, 20/08/2015, 15:48 PM
450
Sự kết thúc của Khoa học
Truyền Bình
Lời nói đầu
Khoa học với tính cách Duy vật, khách quan đang đứng trước cuộc khủng hoảng nghiêm trọng chưa từng có, vì khi Khoa học đi tới chỗ tận cùng của vật thì không thấy vật ở đâu, hoang mang không biết thực tại là gì. Những người theo chủ nghĩa thực chứng (positivism) thì bất cần thực tại, hễ cái gì tôi nhìn thấy, sờ mó được, ăn uống được, cảm nhận được, thì là thực tại. Nhưng thái độ như vậy sẽ không tránh khỏi đau khổ, vì trên đời có vô số sự việc thương tâm: tai nạn, chiến tranh, bệnh tật, áp bức, bất công, tham nhũng, tranh giành…nói chung là đau khổ, thương tâm làm sao giải quyết ? Chẳng hạn tôi biết có một ông thầy dạy môn sinh học, vợ của ông cũng dạy sinh học.
Ông bà có hai đứa con trai, một hôm hai đứa chở nhau đi học, bị tai nạn giao thông chết cả hai. Bà vợ sốc quá phát điên. Ông chồng chẳng những đau khổ vì các con chết hết mà còn phải mang gánh nặng người vợ điên suốt đời. Liệu các khoa học hiện có của con người đã đi tới chỗ giới hạn thì cũng sẽ mở đường cho những khoa học mới như khoa học tâm linh, khoa nhân thể đặc dị công năng hay ngoại cảm học…hay không ? Thật ra thì các khoa học này cũng đã có từ lâu rồi, nhưng chưa được giới khoa học quan tâm, nay họ có sẽ thay đổi thái độ không?
Chúng tôi xin trân trọng cám ơn các tác giả có bài viết trên mạng internet hoặc sách và được trích nhiều trong bài này là : Gs. Phạm Việt Hưng, Tiến sĩ Vật lý Nguyễn Tường Bách, Gs. Cao Chi, Ô. Nguyễn Đức Hiệp,Tướng quân Trương Chấn Hoàn, Ô. Gia Cát Hỷ Hán tác giả sách Siêu Nhân Trương Bảo Thắng, Ký giả Liêu Văn Vĩ tác giả sách Đông Phương Kỳ Nhân, và nhiều người khác. Vì bài quá dài nên xin được ngắt thành 4 phần, đăng thành 4 bài, nhưng có liên quan với nhau.
Dẫn nhập: Sự kết thúc của khoa học khách quan
Nhà báo John Horgan đã viết cuốn sách The End of Science (Sự kết thúc của khoa học) gây nhiều tranh cãi trong giới học thuật.
 |
| John_Horgan_speaking_at_HSS |
 |
Cuốn sách nêu lên một ý nghĩa triết học hơn là ý nghĩa thực tiễn. Ý nghĩa triết học của vấn đề này là, khoa học với với đặc tính trọng yếu là khách quan, duy vật đã đi tới cuối đường và không còn nhiều chỗ để đi nữa. Chứ còn ý nghĩa thực tiễn của khoa học thì vẫn còn nhiều, bởi vì vô số phát minh về khoa học kỹ thuật vẫn có thể tiếp tục khám phá ra những đặc tính mới của vật chất, của sinh học, để chế tạo ra sản phẩm mới, tiện nghi mới cho đời sống thì không bị ảnh hưởng. Nhưng tri thức tổng quát về tính triết học của khoa học thì đã tới giới hạn. Vượt qua giới hạn đó thì sẽ tiến vào khoa học tâm linh.
Cái giới hạn này đã được Thích Ca nêu ra hơn 2500 năm trước trong câu chuyện người mù sờ voi ghi trong Niết Bàn Kinh 涅 槃 经
“有王告大臣，汝牵一象来示盲者时，众盲各以手触。大王唤众盲问之：“汝见象类何物？触其牙者言：象形如萝菔根；触其耳者言如 萁；触其脚者言如臼；触其脊者言如床；触其腹者言如瓮；触其尾者言如绳。……王喻如来正偏知，臣喻方等涅槃经，又象喻佛性，盲者喻一切众生无明也。”
(Có một vị vua nói với đại thần, ngươi hãy dẫn một con voi đến cho bọn mù xem. Những người mù dùng tay để sờ. Vị đại vương kêu bọn mù lại hỏi : “Các ngươi thấy voi giống như vật gì ? Người sờ cái ngà nói : voi giống như cái củ cải. Người sờ lỗ tai nói giống nhánh lá ki. Người sờ chân voi nói giống như cái cối. Người sờ lưng voi nói giống như cái giường. Người sờ bụng voi nói giống như cái lu. Người sờ đuôi voi nói giống như sợi dây thừng… Vua tượng trưng cái biết toàn thể của Như Lai (chánh biến tri 正偏知) Đại thần tượng trưng Kinh Phương Đẳng Niết Bàn. Con voi tượng trưng cho Phật tính. Những người mù tượng trưng cho tất cả chúng sinh vô minh.)
 |
| La bạc căn 萝菔根 (củ cải) |
 |
| Ki 萁 (lá ki) |
 |
| Cữu 臼 (cái cối) |
Người mù không thể biết được cái toàn thể, mà chỉ biết được phần mớ nào đó thôi. Người mù là ai ? Là nhà chính trị, nhà triết học, nhà khoa học, nhà doanh nghiệp, văn nghệ sĩ và cả bàn dân thiên hạ. Nói chung là tất cả chúng sinh, với cái biết của bộ não, họ không bao giờ có thể đạt tới cái biết toàn thể.
Đức Phật kể câu chuyện người mù sờ voi để biểu thị ý tưởng rằng trí óc duy lý của con người là hữu hạn, nó không thể biết được cái toàn thể vì cái hiểu biết của nó dựa trên cơ sở vô minh. Triết học và khoa học của loài người xây dựng trên nền tảng vô minh, không biết rằng bản chất của thế giới là không, không có nghĩa lý gì cả, nếu đi đến hiểu biết tận cùng thì sẽ gặp phải mâu thuẫn, phi logic, lý thuyết trở nên phi lý không thể hiểu được, không thể chấp nhận được.
Nhưng tại sao lại có vấn đề kết thúc, làm sao biết là đã đi đến cuối đường và không còn lối đi nữa ? Chúng ta sẽ nghiên cứu vấn đề này dựa trên ba trụ cột quan trọng nhất của khoa học là : toán học, vật lý học và sinh học.
Sự kết thúc của Toán học
Chúng ta hãy theo dõi tiến trình phát hiện ra sự giới hạn của toán học qua các bài viết của Giáo sư toán Phạm Việt Hưng như sau.
Đã qua rồi cái thời khoa học được coi như những chân lý xác định, chắc chắn, rõ ràng của Tự Nhiên. Tuyên ngôn nổi tiếng của Einstein, “Chúa không chơi trò súc sắc với vũ trụ ” (God does not play dice with the cosmos), đã được hậu thế công khai nói ngược lại: “Chúa không chỉ chơi trò súc sắc trong Cơ học Lượng tử mà còn cả trong nền tảng của toán học”. Người cả gan nói điều ngược lại này là Gregory Chaitin, chuyên gia nổi tiếng của đại tổ hợp IBM, tác giả của những công trình lớn nhất về lý thuyết thông tin thuật toán hiện nay. Sau khi khám phá ra một con số kỳ lạ, được gọi là số Omega hoặc số Chaitin, một số thực (real number) nhưng không thể xác định được, không thể tính được, không tồn tại bất kỳ một chương trình thuật toán nào để đọc các chữ số của nó – Chaitin đã phát hiện ra cái mà Heisenberg đã phát hiện ra trong Cơ học Lượng tử : yếu tố bất định trong toán học.
 |
| Gregory Chaitin |
Thật vậy, các chữ số của Omega xuất hiện một cách ngẫu nhiên theo xác suất! Và không chỉ Omega, còn có hàng loạt những số tương tự mà Chaitin gọi là các số siêu-Omega, siêu-siêu-Omega, siêu-Omega cấp n, v.v. Vì tất cả những số này là số thực, chúng tồn tại, nên Chaitin đưa ra một nhận định làm choáng váng thế giới khoa học : Yếu tố ngẫu nhiên là một đặc trưng của toán học, suy ra toàn bộ khoa học và bản thân thế giới tự nhiên có bản chất ngẫu nhiên! Điều đó có nghĩa là toán học cũng chỉ là chủ quan tùy tiện chứ không thật sự là khách quan.
Trong bối cảnh của những khám phá mới, vấn đề giới hạn của nhận thức càng ngày càng trở thành quan trọng vì nó không chỉ là vấn đề của triết học, mà còn của chính khoa học, ảnh hưởng đến các định hướng nghiên cứu khoa học. Vào thời điểm bản lề chuyển từ thế kỷ 20 sang thế kỷ 21, nó đã trở thành một trong các đề tài nghiên cứu khoa học được chú ý nhất. Đó là lý do ra đời một loạt sách báo về đề tài này, trong đó cuốn sách của Horgan là một cuốn tiêu biểu. Một hội nghị thế giới tập trung các nhà khoa học hàng đầu để bàn thảo vấn đề này đã được tổ chức tại Đại học Santa Fe (Santa Fe Institute), bang New Mexico, Mỹ, vào mùa xuân năm 1995.
Trong gian đại sảnh của hội nghị, đập vào mắt các đại biểu là một tiêu đề lớn: “The Limits of Science Knowledge” (Giới hạn của hiểu biết khoa học). Nhà toán học nổi tiếng John Casti, chủ toạ hội nghị, khai mạc bằng câu hỏi: “Phải chăng thế giới quá phức tạp đối với chúng ta để hiểu nó ?”. Joseph Traub, một nhà khoa học lý thuyết computer bậc nhất, giáo sư Đại học Columbia, đặt câu hỏi cụ thể hơn: “Liệu chúng ta có thể biết cái gì là cái không thể biết hay không? Liệu chúng ta có thể chứng minh rằng khoa học có giới hạn hay không, như Godel và Turing đã chứng minh có những giới hạn đối với toán học và khoa học tính toán ?”.
Trong gian đại sảnh của hội nghị, đập vào mắt các đại biểu là một tiêu đề lớn: “The Limits of Science Knowledge” (Giới hạn của hiểu biết khoa học). Nhà toán học nổi tiếng John Casti, chủ toạ hội nghị, khai mạc bằng câu hỏi: “Phải chăng thế giới quá phức tạp đối với chúng ta để hiểu nó ?”. Joseph Traub, một nhà khoa học lý thuyết computer bậc nhất, giáo sư Đại học Columbia, đặt câu hỏi cụ thể hơn: “Liệu chúng ta có thể biết cái gì là cái không thể biết hay không? Liệu chúng ta có thể chứng minh rằng khoa học có giới hạn hay không, như Godel và Turing đã chứng minh có những giới hạn đối với toán học và khoa học tính toán ?”.
Ngay lập tức cuộc thảo luận bùng nổ. Có nhiều ý kiến vô cùng đặc sắc, thú vị. Chaitin nói : “Thông thường chúng ta hay cho rằng nếu người ta nghĩ cái gì là đúng thì nó phải đúng vì một lý lẽ nào đó. Trong toán học lý lẽ ấy được gọi là một chứng minh, và công việc của nhà toán học là tìm kiếm chứng minh - những lý lẽ, suy luận từ các tiên đề hoặc những nguyên lý được chấp nhận trước. Nhưng hiện nay, cái mà tôi khám phá ra là các chân lý toán học đúng mà chẳng cần phải có một lý do nào cả. Chúng đúng một cách bất ngờ hoặc ngẫu nhiên”.
Nếu Chaitin đúng, hoặc nói cách khác, nếu cái đà lý luận kiểu Chaitin mà phát triển trong khoa học, thì phỏng khoa học còn có ý nghĩa gì nữa? Không, chúng ta khó có thể nhắm mắt chấp nhận ý kiến của Chaitin, nhưng… có lẽ chúng ta cũng không thể nhắm mắt tảng lờ ý kiến của Chaitin. Một lần nữa, chúng ta phải dám “đối mặt với giới hạn của nhận thức”, như John Horgan đề nghị. Điều cần thiết là phải xem xét lại định nghĩa của khoa học? Quan niệm về khoa học kiểu Einstein có còn là một mẫu mực tiêu chuẩn nữa hay không ? Liệu tôi tư duy, tôi có tồn tại không?
Cách đây khoảng bốn chục năm, Jean Paul Sartre từng nói: “Tôi tư duy, vậy tôi không tồn tại”. Hồi đó hình như ít người để ý đến phản đề của Sartre. Decartes từng nói “Tôi tư duy, vậy tôi tồn tại” (Je pense, donc je suis). Còn Sartre nói ngược với Descartes. Và liệu chúng ta có thể đồng ý với Bacon để coi “thiên nhiên như gái điếm” được không? Con người có thể chế ngự Tự Nhiên theo ý muốn của mình hay không? Chúng ta dứt khoát không thể đầu hàng bỏ cuộc, nhưng rõ ràng chúng ta phải xem xét lại hành trang của mình.
John Horgan để lộ quan điểm cá nhân của ông thông qua những người được ông phỏng vấn hoặc những người đã khuất mà ông ngưỡng mộ. Dù sao thì các nhà triết học vẫn có cái nhìn sâu xa hơn các nhà khoa học. Immanuel Kant, nhà triết học Đức lỗi lạc, người có ảnh hưởng lớn đến tư duy khoa học thế kỷ 19, nói : “Mỗi câu trả lời lại làm dấy lên những câu hỏi mới”. Điều này thật dễ hiểu, nó đơn giản nói với chúng ta rằng chẳng bao giờ chúng ta tìm ra chân lý cuối cùng cả. Nhưng nhân loại có tính hay quên. Những bộ óc vĩ đại nhất thường thích đạt tới chỗ thái quá : muốn truy ra cái nguồn gốc ban đầu đến tận gốc rễ. Tác phẩm vĩ đại nhất của Charles Darwin là cuốn “Nguồn gốc các loài”, được coi là một trong hai thành tựu vĩ đại nhất của các thế kỷ trước (cùng với cơ học Newton). Tên gọi cuốn sách này đã lộ rõ khát vọng của nhà bác học : chỉ rõ nguồn gốc ban đầu của sinh giới. Nhưng thực ra chúng ta chẳng bao giờ tìm thấy cái nguồn gốc ban đầu đó cả, không kể ngay cả những nguồn gốc trung gian trong sự tiến hoá cũng chưa phải là hoàn toàn thuyết phục. Horgan đã dành cả một chương trong sách của ông để nói về sinh học tiến hoá: “The End of Evolutionary Biology” (Sự kết thúc của sinh học tiến hoá). Những chi tiết trong chương này chắc chắn rất thú vị với mọi độc giả, dù quan điểm của bạn nghiêng về phía ủng hộ hay chống đối Darwin (ở Mỹ, rất nhiều trường học đã bãi bỏ học thuyết Darwin trong chương trình sinh học).
Một “cú đòn” trời giáng khác mà Horgan làm choáng váng độc giả là chương dành cho vật lý, “The End of Physics” (Sự kết thúc của vật lý), trong đó thể hiện mối nghi ngờ về khả năng thành công của lý thuyết lớn nhất của vật lý ngày nay là “Lý thuyết về mọi thứ”. Trong số những người thẳng thắn bày tỏ mối nghi ngờ đối với lý thuyết này có những người đã có công rất lớn đối với vật lý hiện đại. Một trong số đó là Sheldon Glashow, một trong ba người đoạt giải Nobel vật lý năm 1979 vì một đề tài tiền thân của Lý thuyết về mọi thứ (Lý thuyết điện từ yếu). Glashow gọi Lý thuyết về mọi thứ là “Chiếc Chén Thánh” (The Holy Grail) (chiếc chén Chúa Jesus dùng trong bữa tiệc ly trước khi bị hành hình), ngụ ý đó là một cái gì đó rất thiêng liêng về ý tưởng nhưng không bao giờ có thể biến thành hiện thực ! Một người khác là Roger Penrose, tác giả của những công trình tuyệt tác về topo chứng minh sự tồn tại của điểm kỳ dị của các hốc đen và của toàn bộ không-thời-gian, làm cơ sở cho Lý thuyết Big Bang. Penrose nói rõ rằng ông không tin vào bất cứ một lý thuyết nào hiện nay, kể cả Lý thuyết siêu dây, có thể coi là có hy vọng tiến đến Lý thuyết về mọi thứ.
Nếu nhận thức được ý nghĩa của tất cả những thách thức đó, khoa học buộc phải định hướng phát triển thông minh nhất, sao cho có thể dồn nỗ lực vào những nghiên cứu có hiệu quả nhất, thiết thực nhất.
Để làm được điều đó, câu hỏi của Joseph Traub có lẽ là câu hỏi quan trọng nhất. Xin nhắc lại: “Liệu chúng ta có thể biết cái gì là cái không thể biết hay không?”.
Câu hỏi này làm chúng ta nhớ lại một lời dạy của Khổng tử: “Tri chi vi tri chi, bất tri vi bất tri, thị tri dã” (Cái gì biết thì biết là mình biết, cái gì không biết thì biết là mình không biết, đó là biết vậy). Thật kỳ lạ, hơn 25 thế kỷ trước, bằng kinh nghiệm và trực giác thiên tài, ông thánh Phương Đông này đã khẳng định nhận thức có giới hạn, và hiểu được điều này mới thực sự là có nhận thức. Và 25 thế kỷ sau, bằng con đường phân tích mổ xẻ đến nơi đến chốn, khoa học cũng đi đến nhận định tương tự, nhưng cụ thể hơn:
Cần phải tìm hiểu xem cái gì là cái không thể biết.
Kurt Godel với Định lý Bất toàn (Theorem of incompleteness) đã làm điều đó với Toán học.
Alan Turing với Sự cố Dừng (The Halting Problem) đã làm điều đó với khoa học tính toán.
Hậu thế sẽ phải tiếp tục con đường của Godel và Turing để làm điều tương tự đối với vật lý, sinh học, và khoa học nói chung.
Dẫu rằng nhiệm vụ này vô cùng khó khăn, nhưng dẫu sao nó cũng đã đánh một tiếng chuông cảnh tỉnh đối với khoa học, khuyến dụ khoa học phải tỉnh táo hơn trên con đường phát triển.
Và nó có một phản ứng phụ tích cực: Vì không bao giờ có thể đi đến một lý thuyết cuối cùng trong bất kỳ lĩnh vực tri thức nào, do đó các nhà khoa học sẽ không bao giờ thất nghiệp; ngược lại họ sẽ luôn luôn phải bận rộn với những bài toán chưa giải được để giải, bởi vì vĩnh viễn sẽ tồn tại rất nhiều bài toán như thế. Chỉ có điều cần phải chú ý đến những bài toán đáp ứng với quyền lợi thiết thực của con người nhiều hơn, thay vì nhất định đòi hiểu được ý Chúa.
Tóm lại, cuốn sách của Horgan không hề khiêu khích hay nổi loạn, ngược lại nó khuyến khích chúng ta tư duy một cách thiết thực hơn!
Ngay từ thế kỷ 18, Immanuel Kant đã nói: “Hình học dựa trên trực giác không gian; Số học dựa trên trực giác thời gian”.
Bước vào thế kỷ 20, David Hilbert phủ nhận Kant một cách tuyệt đối. Ông cho rằng toán học thực chất là các quan hệ logic, do đó những quan hệ này càng được hình thức hoá cao bao nhiêu thì toán học càng chính xác bấy nhiêu. Nói cách khác, toán học không phải là một khoa học thực dụng như vật lý, hoá học, bởi nó không nghiên cứu bản chất vật chất của các đối tượng, mà chỉ nghiên cứu mối quan hệ logic giữa các đối tượng đó mà thôi. Nếu toán học vấp phải nghịch lý, ấy là vì toán học trước đây vẫn còn vướng quá nhiều “bụi trần”, tức là chưa thật sự toán học, chưa thật sự là một hệ logic thuần tuý hình thức. Muốn có một nền toán học chân chính, phải giải phóng toán học một cách tuyệt đối khỏi thế giới hiện thực, phải hình thức hoá toán học một cách tuyệt đối từ nền móng cho tới thượng tầng. Muốn vậy, phải xây dựng lại toàn bộ cơ sở của toán học, hướng tới mục tiêu cuối cùng là hệ thống “siêu-toán-học” (metamathematics) – một hệ thống logic tuyệt đối siêu hình, hoàn toàn độc lập với thế giới hiện thực, cho phép giải thích và chứng minh mọi mệnh đề toán học cho tới cùng kỳ lý, loại trừ hoàn toàn mọi nghịch lý, mâu thuẫn. Hilbert tin chắc rằng với một phương pháp nghiên cứu đúng đắn, trước sau toán học sẽ đạt tới mục tiêu đó. Câu châm ngôn nổi tiếng của ông, “Chúng ta phải biết, Chúng ta sẽ biết” (Wir müssen wissen, wir werden wissen), được khắc trên bia mộ ông đã nói lên tham vọng “vá trời lấp biển” của ông.
 |
| David Hilbert |
Để chứng minh tư tưởng của mình là đúng và khả thi, bản thân Hilbert đã bỏ công xây dựng lại Hình Học Euclid. Xuất phát từ một hệ 20 tiên đề, ông đã xây dựng nên một thứ hình học thuần tuý hình thức, không cần hình vẽ, được gọi là Hình Học Hilbert, ra mắt năm 1899 dưới tên gọi Cơ Sở Hình Học (Grundlagen der Geometrie). Nhưng không thoả mãn với những gì đã làm được, Hilbert kêu gọi toàn thế giới toán học cùng bắt tay vào việc tái thiết toà lâu đài toán học theo “thiết kế” của Chủ Nghĩa Hình Thức.
Mục tiêu tiếp theo là Số Học: Hãy xây dựng cho số học một hệ tiên đề hình thức đầy đủ, độc lập, phi mâu thuẫn, để từ đó xây dựng nên một lý thuyết số học tuyệt đối hình thức. Đó chính là nội dung cơ bản của Bài Toán Số 2 trong số những bài toán ông nêu lên tại Hội Nghị Toán Học Thế Giới ở Paris năm 1900, như một thách thức đối với toán học thế kỷ 20.
Với uy tín lừng lẫy của bản thân, Hilbert đã tập hợp được phần lớn các nhà toán học đương thời dưới ngọn cờ của mình, bao gồm cả một kẻ thù vốn không đội trời chung với ông về hình học, đó là Gottlob Frege.
 |
| Gottlob Frege |
Thật vậy, Frege đồng ý với Kant rằng hình học dựa trên trực giác, và do đó đã quyết liệt chống đối Hilbert trong ý tưởng biến hình học thành một mớ logic hình thức thuần tuý. Nhưng trớ trêu thay, Frege lại đồng quan điểm với Hilbert khi cho rằng số học dựa trên logic, do đó đã trở thành cứu tinh của Hilbert về mặt số học: Frege đã lao vào làm một cuộc cách mạng về số học, nhằm biến số học thành một hệ logic hình thức thuần tuý, đúng như Hilbert mong muốn!
Để làm cuộc cách mạng đó, Frege bắt đầu xây dựng lại số học từ nền móng – định nghĩa lại khái niệm về số. Với Frege, từ nay số 2 không được hiểu một cách “tầm thường” là 2 con gà, 2 con vịt, … mà phải hiểu là tập hợp của các cặp đôi (pairs); 3 là tập hợp của các “bộ 3” (triples), một cách tổng quát, số là tập hợp của các tập hợp.
Định nghĩa ấy thể hiện tham vọng chính xác hoá các khái niệm toán học đến vô chừng vô độ: Frege đã tìm mọi cách “tẩy rửa”, vứt bỏ mọi ý nghĩa dính dáng đến vật chất cụ thể của số, vì chừng nào số còn gắn với ý nghĩa vật chất cụ thể thì chừng ấy số vẫn chứa đựng bên trong nó những “hạt sạn phi-toán-học” – nguồn gốc dẫn tới nghịch lý mâu thuẫn. Một nhà toán học đã bình luận rằng với Frege, 3 không phải là “number three” (số 3), mà là “the threeness” (cái 3) (!).
Sau khi thanh tẩy và hình thức hoá tuyệt đối các khái niệm cơ sở của của số học, Frege đã xây dựng nên hàng trăm định lý của số học dưới dạng hình thức tuyệt đối. Toàn bộ lý thuyết của ông đã được công bố trong bộ sách đồ sộ mang tên Cơ Sở Số Học (Grundlagen der Arithmetik), một bộ sách đã làm rung chuyển thế giới toán học. Thật vậy, các nhà toán học theo Chủ Nghĩa Hình Thức đã thật sự bị choáng ngợp trước “vẻ đẹp siêu thoát tinh tuyển hình thức” trong lý thuyết của Frege. Họ phấn chấn đến mức tưởng rằng sắp tìm thấy “Chiếc Chén Thánh”, và tưởng rằng “thiên đường của chủ nghĩa hình thức” đã lấp ló đâu đó ở phía chân trời!
Đó là lúc cuộc đời Frege đạt tới tột đỉnh vinh quang. Tên tuổi của ông nổi lên như sóng cồn. Người ta gọi ông là “ngọn đèn pha của Chủ Nghĩa Hình Thức”. Cuốn Cơ Sở Số Học của ông được tôn vinh như một kiệt tác toán học, sánh vai với những tác phẩm toán học vĩ đại khác, như bộ Cơ Sở của Euclid chẳng hạn, và thậm chí được ca ngợi như cuốn “Kinh Koran của chủ nghĩa logic hình thức”, … (!)
Trớ trêu thay, ngay lúc đó một cú sốc khủng khiếp xảy ra, người vạch ra sai lầm của Frege lại là người vốn ngưỡng mộ Frege hết lòng: Đó là Bertrand Russell (1872-1970), một người luôn luôn khao khát tìm kiếm chân lý tuyệt đối của toán học như một con chiên ngoan đạo khao khát đức tin tôn giáo.
Trong cuốn “Portraits from Memory” (Những chân dung qua trí nhớ) Russell viết: “Tôi khao khát tìm kiếm cái chắc chắn (certainty) giống như người ta khao khát đức tin tôn giáo. Tôi nghĩ tính chắc chắn dường như có trong toán học nhiều hơn ở bất kỳ nơi nào khác”. Với tư tưởng đó, Russell đã nghiễm nhiên gia nhập “phái nền tảng” (foundationism) – trường phái đòi xét lại nền tảng của toán học đầu thế kỷ 20. Phái này cũng chính là “phái hình thức” (formalism), bởi họ cho rằng muốn xây dựng lại toán học, phải triệt để hình thức hoá toàn bộ toán học, biến toán học thành một hệ logic tuyệt đối siêu hình, hoàn toàn tách rời thế giới hiện thực, như Russell tuyên bố: “Toán học là một khoa học mà trong đó người ta không bao giờ biết người ta đang nói về cái gì, miễn là cái điều người ta nói là đúng”. Chẳng hạn, khi xét mệnh đề 2 + 3 = 5, toán học “chân chính” không cần biết ý nghĩa vật chất cụ thể của các số 2, 3, 5 là cái gì, miễn là có được những định nghĩa và tiên đề nào đó về số cho phép kiểm tra mệnh đề đã cho là đúng hay sai. Chính vì khao khát nhận biết được cái “thế giới siêu việt” ấy nên Russell đã bàng hoàng xúc động khi đọc Cơ Sở Số Học của Frege, coi Frege như một ngôi sao dẫn đường của toán học hình thức.
Nhưng rồi Russell khám phá ra một nghịch lý.
Russell chia tập hợp thành hai loại:
1* Tập thông thường (ordinary set), là tập hợp sao cho nó không phải là phần tử của chính nó (nó không thuộc chính nó). Thí dụ: Tập hợp những chiếc xe máy là một tập thông thường, vì tập hợp ấy không thể là một chiếc xe máy.
2* Tập lạ thường (extraordinary set), là tập hợp sao cho nó là phần tử của chính nó (nó thuộc chính nó). Thí dụ: Tập hợp của tất cả những gì không phải là chiếc xe máy. Dễ thấy tập hợp này là một phần tử của chính nó, vì tập hợp này không phải là một chiếc xe máy.
Có rất nhiều tập thông thường khác nhau cũng như có rất nhiều tập lạ thường khác nhau. Russell đề nghị xét một tập hợp đặc biệt, đó là Tập hợp của tất cả các tập thông thường. Ví dụ tập hợp của tất cả các tập hợp xe máy (đặt tên là Tập Russell) là thông thường hay lạ thường ? Ngay lập tức, cái đầu logic sắc sảo của Russell dẫn ông tới một nghịch lý :
Giả sử Tập Russell là tập thông thường, lập tức suy ra nó là một phần tử của chính nó (vì Tập Russell chứa tất cả các tập thông thường). Nhưng nếu nó là một phần tử của chính nó thì nó phải là tập lạ thường, vậy Tập Russell là tập lạ thường, mâu thuẫn với giả thiết!
Giả sử Tập Russell là tập lạ thường, cũng mâu thuẫn với giả thiết tương tự như vậy!
Kết luận:
Nếu Tập Russell là tập thông thường thì nó sẽ là tập lạ thường.
Nếu Tập Russell là tập lạ thường thì nó sẽ là tập thông thường.
Đó chính là Nghịch lý Russell, để cho dễ hình dung, Russell đã sáng tác câu chuyện ông thợ cạo như sau : Ngày xưa, có 1 ông thợ cạo, được nhiều người cho rằng sống ở làng Seville. Tại làng đó, tất cả đàn ông đều tự cạo râu hoặc nhờ thợ cạo. Và ông thợ này đã tuyên bố: “Tôi chỉ cạo râu cho những người đàn ông nào của làng Seville mà không tự cạo râu”.
Như vậy nam nhi của làng Seville chia làm hai nhóm : nhóm 1 tự cạo râu, nhóm 2 không tự cạo râu. Rắc rối là không biết xếp ông thợ cạo vào nhóm nào, vì : nếu xếp ông vào nhóm 1 thì ông không được tự cạo râu cho ông, mà không tự cạo râu thì phải xếp ông vào nhóm 2, mà nếu vậy thì sẽ được cạo râu, mà đã được cạo râu thì phải xếp vào nhóm 1. Xếp cách nào cũng mâu thuẫn với tiên đề, nên mới gọi là nghịch lý.
Ngày 16-06-1902, Bertrand Russell gửi tới Frege một lá thư, trong đó có đoạn viết: “Trong công trình của ngài, tôi tìm thấy những lý thuyết đẹp đẽ nhất trong thời đại của chúng ta mà tôi biết, và do đó tôi tự cho phép mình bầy tỏ một sự kính trọng sâu xa đối với ngài”
Rồi Russell thông báo cho Frege biết nghịch lý của mình với một thái độ rất tao nhã, khiêm tốn: “Tôi tán thành với ngài về mọi điểm, nhưng chỉ có một điểm tôi gặp phải khó khăn …”.
Nhưng trong khi Russell khiêm tốn như thế thì chính Frege lại nhanh chóng nhận thấy nguy cơ sụp đổ toàn bộ công trình của đời mình.
Với bản chất trung thực, thẳng thắn hiếm có, ông lập tức viết thư trả lời Russell, và viết ngay một phụ lục bổ sung vào Tập 2 của bộ Cơ Sở Số Học, đúng vào lúc nó chuẩn bị được đem in, như một sự công khai thừa nhận thất bại của mình: “Không còn gì tồi tệ hơn có thể xẩy đến với một nhà khoa học khi phải chứng kiến nền tảng lý thuyết của mình sụp đổ đúng vào lúc công trình được hoàn thành. Tôi đã bị đặt vào tình thế này do vừa nhận được một lá thư từ ngài Bertrand Russell”.
Nhà khoa học có thể gặp nhiều nỗi cay đắng, nhưng hiếm có nỗi cay đắng nào giống như của Frege: Ông mất năm 1925 với tâm trạng của một kẻ tin rằng công trình của cả cuộc đời mình chỉ dẫn tới sự vô ích. Cái chết của ông không được cộng đồng khoa học biết tới.
Nếu lòng dũng cảm và tính trung thực là thước đo nhân cách của một nhà khoa học thì Gottlob Frege (1848-1925) phải được coi là một trong những nhà khoa học có nhân cách vĩ đại nhất: Mặc dù cay đắng đến tột cùng khi tác phẩm để đời của ông – cuốn Cơ Sở Số Học - bị sụp đổ tan tành chỉ vì một nghịch lý đã được phát hiện ngay trong nền tảng lý thuyết, nhưng Frege không tìm cách né tránh hoặc ngụy biện, mà ngược lại, đã xử sự như một người quân tử: Công khai thừa nhận sai lầm và dứt khoát từ bỏ lý tưởng toán học hình thức mà ông đã ấp ủ cả cuộc đời. Một năm trước khi mất, ông để lại những lời trăng trối vô cùng cảm động, như một lời sám hối về nhận thức sai lầm đối với bản chất của toán học.
Có hai phương án giúp giải quyết nghịch lý này được đề xuất vào năm 1908. Một trong số đó là thuyết loại hình do Russell đề xuất, và thứ hai là thuyết tập hợp Zermelo, điều chỉnh lại tiên đề để loại trừ mâu thuẫn và sau cùng phát triển thành thuyết tập hợp Zermelo–Fraenkel (ZF).
Khi ta xét tập hợp : “S là tập hợp của tất cả các tập hợp” để rồi gặp phải tình huống: “Một phần tử thuộc hoặc không thuộc tập S đều dẫn đến mâu thuẫn”. Sau đó, để tránh sai lầm trên, người ta không dùng thuật ngữ “tập hợp của tất cả các tập hợp” mà đề xuất một khái niệm mới, tổng quát hơn là “lớp”. Trong đó, người ta chỉ cần khoanh vùng một tập hợp bao gồm đủ nhiều các tập hợp nào đó (nhưng không phải là tất cả) để làm việc thì sẽ không phải gặp mâu thuẫn nữa.
Thay vì linh cảm mách bảo nghịch lý chính là tín hiệu báo động bản chất bất toàn của mọi hệ logic (như sau này Định lý Gödel đã chỉ rõ), phần lớn các nhà toán học đã tập hợp lại dưới ngọn cờ của David Hilbert để lo sửa chữa, tái thiết lại toà lâu đài toán học, với nhiệm vụ cấp bách là làm “vệ sinh” cho toán học – “tẩy rửa” mọi nghịch lý ra khỏi toán học!
Đó là lý do ra đời Chương Trình Hilbert, với tham vọng “vá trời lấp biển”: Xây dựng một hệ thống siêu-toán-học (meta-mathematics) – một hệ thống toán học tuyệt đối siêu hình, tuyệt đối thoát ly khỏi thế giới hiện thực, cho phép XÁC ĐỊNH tính trắng/đen, đúng/sai của bất kỳ một mệnh đề toán học nào và chứng minh tính phi mâu thuẫn của toàn bộ toán học.
Để xây toà lâu đài siêu-toán-học, cần có những công cụ lý tưởng, nhằm đảm bảo tuyệt đối loại bỏ các “tạp chất phi-toán-học” ra khỏi toán học. Công cụ “lý tưởng” ấy đã sẵn có: Logic và lý thuyết tập hợp, như Hermann Weyl mô tả : “Logic là phép vệ sinh mà các nhà toán học thực hành nhằm giữ cho tư tưởng của họ được khoẻ mạnh và chắc chắn”. Kể từ đó, chủ nghĩa tôn sùng logic và tập hợp ra đời, nghiễm nhiên trở thành tư tưởng thống trị toán học, rồi dần dần trở thành một “mốt thời thượng”, cứ như là nếu không có logic và tập hợp thì toán học sẽ tiêu vong (!?).
Nhưng Lễ hội tưng bừng” của Chương Trình Hilbert bị chấm dứt đột ngột khi Gödel công bố Định Lý Bất Toàn (Theorem of Incompleteness) : “Năm 1931, một nhà toán học mới có 25 tuổi đã công bố một công trình vĩnh viễn phá huỷ niềm hy vọng của Hilbert. Kurt Gödel đã buộc các nhà toán học phải chấp nhận rằng toán học sẽ không bao giờ hoàn thiện về mặt logic, …Đây là một đòn chí mạng giáng vào chương trình Hilbert”.Hoá ra “giấc mộng vàng” của Chương Trình Hilbert chỉ là một giấc mơ không tưởng. Cả Hilbert lẫn Frege đều đã bị chứng minh là nhầm lẫn. Định Lý Bất Toàn của Kurt Gödel đã phủ nhận toàn bộ chương trình Hilbert, phủ nhận toàn bộ công trình hình thức hoá số học của Frege cho thấy lý tưởng của Chủ Nghĩa Hình Thức chỉ là một ảo tưởng hão huyền – một cái vòng luẩn quẩn của kẻ đi tìm điểm cuối trên một đường tròn!
Nội dung của Định Lý Bất Toàn:
Nguyên văn Định Lý của Kurt Gödel được trình bầy bằng ngôn ngữ logic hình thức, rất khó hiểu đối với những người không chuyên ngành. Nhưng may thay, nó đã được phiên dịch sang ngôn ngữ thông thường để bất cứ ai cũng có thể hiểu được. Gọi chung là Định Lý Bất Toàn nhưng thực ra có hai định lý. Cả hai đều chỉ ra rằng toán học về bản chất là bất toàn (không đầy đủ), vì nó luôn chứa đựng những mệnh đề không quyết định được (undecidable), tức những mệnh đề không thể chứng minh và cũng không thể bác bỏ.
 |
Định lý 1: Nếu một lý thuyết dựa trên một hệ tiên đề phi mâu thuẫn thì trong lý thuyết ấy luôn luôn tồn tại những mệnh đề không thể chứng minh cũng không thể bác bỏ.
Định lý 2: Không tồn tại bất cứ một quy trình suy diễn nào cho phép chứng minh tính phi mâu thuẫn của một hệ tiên đề.
Chẳng hạn, hãy xét mệnh đề được tô đậm sau đây:
Mệnh đề này không có bất cứ một chứng minh nào
Nếu mệnh đề trên sai, suy ra phủ định của nó đúng, tức là nó có thể chứng minh được, nhưng kết luận này trái với nội dung của chính nó. Vậy buộc nó phải đúng, tức là không thể chứng minh được.
Ý nghĩa triết học của Định lý bất toàn
-Kết luận chủ yếu của Wittgenstein, rằng “logic là cần chứ không đủ để mô tả bất kỳ một thực tế khách quan nào”, và rằng “ngôn ngữ không thể bắt kịp với tất cả những gì tồn tại trên thế giới”, đã được Gödel trình bầy dưới dạng toán học … Về căn bản, cái mà Godel chỉ ra là không có một dạng toán học nào có thể đủ thông minh để biểu hiện đầy đủ khái niệm chân lý thường ngày.
-Thế giới chân lý có thể chứng minh được quá nhỏ so với thế giới chân lý có thể nhận thức được (bằng trực giác + mọi phương tiện nhận thức), nhưng thế giới chân lý nhận thức được lại quá nhỏ bé so với thế giới hiện thực.
 |
Có nghĩa là thế giới hiện thực quá mênh mông so với thế giới có thể chứng minh được! Vì thế Gödel không thể cầm lòng mà thốt lên:
“My God, the mazes must be enormous!” (Ôi lạy Chúa, cái mê cung (Ngài tạo ra) mới khổng lồ làm sao!). Lời thán này làm ta nhớ đến lời thán của Pierre Simon de Laplace một thế kỷ trước: “Ce que nous savons est peu de choses, ce que nous ignorons est immense” (Cái ta biết thì quá ít ỏi, cái ta không biết thì mênh mông). Nhưng Laplace chỉ nói như một tâm sự triết lý, trong khi Gödel nói như một khẳng định khoa học! Đó không phải là chủ nghĩa “bất khả tri” (Agnosticism), mà là khoa học về giới hạn của nhận thức.
-Sau này Alan Turing đã đưa ra một diễn giải những kết quả của Godel bằng cách đặt chúng trên một cơ sở thuật toán: Có những con số và hàm số không thể tính toán được bằng bất kỳ một chiếc máy logic nào.
-Gần đây hơn, Gregory Chaitin, một nhà toán học làm việc tại IBM, đã nhấn mạnh rằng những kết quả của Godel và Turing đã xác định những giới hạn cơ bản đối với toán học.
-Là một trong những nhà logic xuất sắc nhất của mọi thời đại, Gödel với công trình của ông đã gây ra một va chạm vô cùng lớn đối với tư duy khoa học và triết học thế kỷ XX, vào lúc mà rất nhiều người, như Bertrand Russell, Alfred Whitehead và David Hilbert đang cố sử dụng logic và lý thuyết tập hợp để hiểu được toàn bộ nền tảng của toán học.
-Định lý Gödel đã chấm dứt một nỗ lực kéo dài một trăm năm hòng thiết lập một hệ tiên đề cho toàn bộ toán học. Nỗ lực chủ yếu đã được thực hiện bởi Bertrand Russell trong cuốn Principia Mathematica(1910-1913). Một nỗ lực khác là chủ nghĩa hình thức của Hilbert, nhưng những nỗ lực này đã bị giáng một đòn chí tử bởi những kết quả của Gödel.
-Định lý Gödel là một bước ngoặt trong toán học thế kỷ 20, chỉ ra rằng toán học không phải là một cái gì đó hoàn hảo như ta vẫn tưởng. Định lý này cũng được sử dụng để ngụ ý rằng không bao giờ có thể lập được một chương trình cho computer để trả lời mọi câu hỏi toán học.
Sự Cố Dừng computer (the halting problem) của Alan Turing
5 năm sau khi Gödel công bố định lý bất toàn, nhà toán học Anh, Alan Turing xây dựng một công trình dựa trên công trình của Gödel. Sử dụng một computer giả thuyết, Turing chỉ ra rằng có một cái gì đó không thể tính toán được: Không thể có một chỉ dẫn nào cho computer để nó có thể tiên đoán một chương trình cho trước sẽ chạy mãi mãi họăc dừng lại. Muốn biết một chương trình liệu cuối cùng có dừng lại hay không, bạn phải đợi một ngày, hoặc một tuần, hoặc một tỷ năm, hoặc tiếp tục chạy chương trình đó mãi mãi và kiên trì chờ đợi. Turing gọi sự cố này là Sự Cố Dừng (The Halting Problem).
Vài thập kỷ sau, trong những năm 1960, Chaitin tiếp tục nghiên cứu Sự Cố Dừng. Ông xét tất cả các chương trình có thể có mà chiếc computer giả thuyết của Turing có thể chạy, rồi tìm xác suất để một chương trình chọn ngẫu nhiên trong số tất cả những chương trình có thể có, sẽ dừng lại. Sau gần 20 năm nghiên cứu, cuối cùng Chaitin chỉ ra rằng “xác suất dừng” do ông nêu lên đã biến Sự Cố Dừng của Turing thành vấn đề tìm một số thực nằm trong khoảng từ 0 đến 1.
Chaitin gọi số đó là Omega và kết luận: Nếu không thể tiên đoán một chương trình cho trước sẽ dừng hay không thì cũng không thể có một chương trình nào cho phép xác định được các chữ số của Omega - Omega là một số không thể tính được hoặc không thể biết được (unkowable)!
Có những con số tuy rất dài nhưng vẫn có thể tính được nếu tồn tại một chương trình hữu hạn cho phép xác định lần lượt từng chữ số của nó đến chừng nào còn có thể tiếp tục công việc, vấn đề chỉ là thời gian và khả năng cho phép của computer. Chẳng hạn Pi (p) là một số vô tỷ – một số thập phân vô hạn không tuần hoàn – nhưng vẫn có thể tính được, vì có một chương trình cho phép xác định mọi chữ số của nó đến chừng nào mà thời gian và khả năng của computer cho phép. Nhưng không có một chương trình nào tương tự như thế đối với Omega: Trong hệ nhị phân, Omega gồm một dãy vô hạn các chữ số 0 và 1 xuất hiện một cách ngẫu nhiên. “Omega không có một hình mẫu hoặc một cấu trúc nào cho nó. Đó là một dãy vô hạn các chữ số 0 và 1 mà mỗi chữ số sau chẳng liên hệ gì với chữ số đứng trước, giống như gieo các đồng xu liên tiếp nhau vậy”, Chaitin nói.
Tóm lại, quá trình dẫn Chaitin tới kết luận Omega là một con số không thể biết cũng tương tự như quá trình dẫn Turing tới kết luận Sự Cố Dừng là không thể biết chắc được. “Đó là thí dụ đặc sắc về một cái gì đó không thể biết trong toán học”, Chaitin nói.
Công trình của Chaitin đã mở ra một hướng mới trong toán học, vật lý và khoa học computer: Nghiên cứu computer lượng tử nhằm vượt qua Sự Cố Dừng, tức là tìm cách “biết cái không thể biết” (to know the unknowable). Đó là một trong các lĩnh vực mũi nhọn của khoa học hiện đại, nơi các trung tâm khoa học cự phách nhất của thế giới đang chạy đua ráo riết để bứt phá, nhằm vượt qua cái ngưỡng không thể vượt qua của computer hiện tại. Trong cuộc chạy đua này, có một nhà khoa học Úc gốc Việt, Giáo sư Kiều Tiến Dũng tại Đại Học Swinburne, Melbourne, Australia, đã đạt được những thành tựu làm sửng sốt giới khoa học tính toán toàn thế giới.
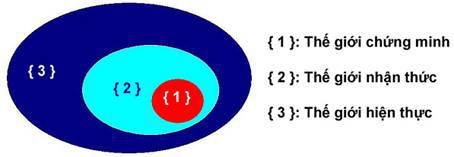
Tóm lại, ý nghĩa triết học quan trọng nhất mà con người ngày nay đã khám phá, đó là toán học chỉ là một công cụ hữu dụng trong một phạm vi giới hạn nào đó thôi. Ngoài phạm vi đó, các phương trình toán học, các đẳng thức là bậy bạ, vô nghĩa, vô dụng. Nhìn vào sơ đồ về 3 thế giới ở trên thì thấy thế giới hữu hiệu của toán học là nhỏ bé so với thế giới hiện thực.
Ví dụ : a/ 2 vợ chồng + 1 đứa con = 3 người (đúng)
b/ 1 hình chồng + 1 hình vợ + 1 hình con = 3 hình (bất toàn theo định lý của Godel, không thể cho là đúng, cũng không thể bác bỏ)
Đẳng thức b/ bất toàn vì hình có thể sản sinh ra không hạn chế.
Đẳng thức 2+1 = 3 với ý nghĩa : vế đầu là số hình họ có, vế sau là số hình mà họ có thể tặng. Đẳng thức đó là bất toàn, vì với 3 tấm hình của 2 vợ chồng và 1 đứa con, họ có thể gởi thành bao nhiêu tấm hình cho bao nhiêu người cũng được (qua mạng internet) 10 người, 100 người, 1000 người, đều được chứ không phải chỉ gởi được 3 tấm hình cho 3 người.
Nói đẳng thức a/ đúng là cũng chỉ tạm đúng trong nhận thức thông thường của con người, chứ Phật pháp còn biết rằng số lượng vật chất cũng chỉ là ảo tưởng. Ta tạm gọi tên chồng là A, vợ là B, con là C, Phật nói rằng trong tam giới có vô lượng vô số A, B, C đồng thời tồn tại giống như hạt photon có thể xuất hiện đồng thời ở hai, ba, bốn, n, vô cực vị trí khác nhau, tất cả chỉ là ảo mà thôi, không khác gì trường hợp b/ Như vậy, đẳng thức, phương trình toán học, số lượng không có nghĩa lý gì cả.
Trong cuộc sống đời thường, có số lượng nào vô nghĩa không ? Xin thưa là có, số lượng không khí mà mỗi người chúng ta sử dụng, vì không khí có rất nhiều nên chẳng ai cần tính số lượng không khí mình thở. Số lượng bit thông tin mà người thuê bao trọn gói sử dụng hàng tháng cũng vô nghĩa, không cần tính. Như vậy chúng ta thấy rằng chính sự hạn chế phát sinh ra số lượng và phát sinh ra toán học. Nếu toán học muốn thoát khỏi sự hạn chế tức là đi ngược với nguyên lý phát sinh của nó, điều đó cũng có nghĩa là sự kết thúc của toán học.
Truyền Bình
CÙNG NHAU XIỂN DƯƠNG ĐẠO PHẬT
Tuân theo truyền thống Phật giáo, chúng tôi cung cấp tài liệu giáo dục Phật giáo phi lợi nhuận. Khả năng duy trì và mở rộng dự án của chúng tôi hoàn toàn phụ thuộc vào sự hỗ trợ của bạn. Nếu thấy tài liệu của chúng tôi hữu ích, hãy cân nhắc quyên góp một lần hoặc hàng tháng.
STK: 117 002 777 568
Ngân hàng Công thương Việt Nam
(Nội dung: Họ tên + tài thí Xiển dương Đạo Pháp)
Ý kiến của bạn
TIN LIÊN QUAN
Dành cho bạn
Phật giáo Việt Nam và sự dung hợp tam giáo thời Trần
Nghiên cứu
14:00 30/11/2024
Có thể thấy, Phật giáo - Nho giáo và Đạo giáo đã có sự dung hòa, bổ sung cho nhau để cùng hướng đến xây dựng đời sống tinh thần và đời sống nhân văn cho xã hội.
Ứng dụng triết lý Phật giáo Trúc Lâm trong xây dựng, phát triển đất nước
Nghiên cứu
08:45 25/11/2024
Phật giáo là cuộc sống, không có sự phân biệt bất cứ thành phần nào trong xã hội, Phật giáo chính là quá trình đi tìm chân lý. Chân lý thì không nằm trong Phật giáo mà nằm trong cuộc sống.
Thiền phái Trúc Lâm Yên Tử: Dấu ấn của Phật giáo thời Trần
Nghiên cứu
09:40 15/11/2024
Thời đại nhà Trần, không những độc lập dân tộc, tự chủ về đời sống kinh tế, chính trị, xã hội…, mà còn độc lập, tự chủ về hệ tư tưởng làm chỗ dựa cho đời sống tinh thần của nhân dân Đại Việt thế kỷ XIII – XIV.
Tín ngưỡng thờ phụng đức Phật Dược Sư thời nhà Đường
Nghiên cứu
09:45 03/11/2024
Việc thiết lập đàn tràng và tu trì đức Phật Dược Sư trở nên quan trọng hơn dưới thời trị vì của vua Đường Túc Tông, thời kỳ triều đình nhà Đường phải vật lộn để vượt qua thách thức do những cuộc nổi dậy của quân đội trong nước gây nên...
Xem thêm
